Breadth-First Search in Elixir
The holidays are over, and I wanted to share one of the things I dedicated myself to during them.
Fun[ctional] holidays

Typically, I take vacations as a time to relax and disconnect from everything work-related. To a computer scientist like me, that means distance from the keyboard, tech books, tech blogs, podcasts, hackernews, lobsters, twitter, etc.
Most of the times I travel or get myself involved in sports activities like biking or hiking, or manual labor like upgrading my bike or ax-cutting a massive, full-grown Cupania vernalis struck by lightning into firewood for winter.
This time, however, I decided to stay home and learn a new programming language. Elixir was on my list for months, and I thought it was about time to remove it from the top. I just had no idea I’d soon fall in love with it.
Elixir is fun 💜
After more than a year away from HackerRank, I found myself back at it, having fun with some easy problems to help me find my way through Elixir’s intricate curves and slopes. After a few of them, I started to enjoy its syntax and to be particularly fond of its pattern matching and immutability. Besides that, it’s not every day I get the chance to play with a functional language.
Not only fun, Elixir is beautiful. Out of a sudden, you start writing elegant solutions to problems:
defmodule JumpingOnTheClouds do
def main do
IO.gets("")
IO.gets("")
|> String.trim()
|> String.split(" ")
|> Enum.map(&String.to_integer/1)
|> jumps
|> IO.puts()
end
defp jumps(clouds), do: jumps(clouds, 1)
defp jumps([_], _), do: 0
defp jumps([_, _], jump), do: rem(jump, 2)
defp jumps([cloud | clouds], 1), do: 1 + jumps(clouds, 2 - cloud)
defp jumps([_, cloud | clouds], 2), do: 1 + jumps(clouds, 2 - cloud)
end
JumpingOnTheClouds.main()
The problem(s)

As things progressed, I started to get a bit more serious and ventured into medium challenges, such as Castle on the Grid and Shortest Reach. I solved both with breadth-first search and was surprised to know that, at the time of this writing, I was the only one to do so with Elixir:
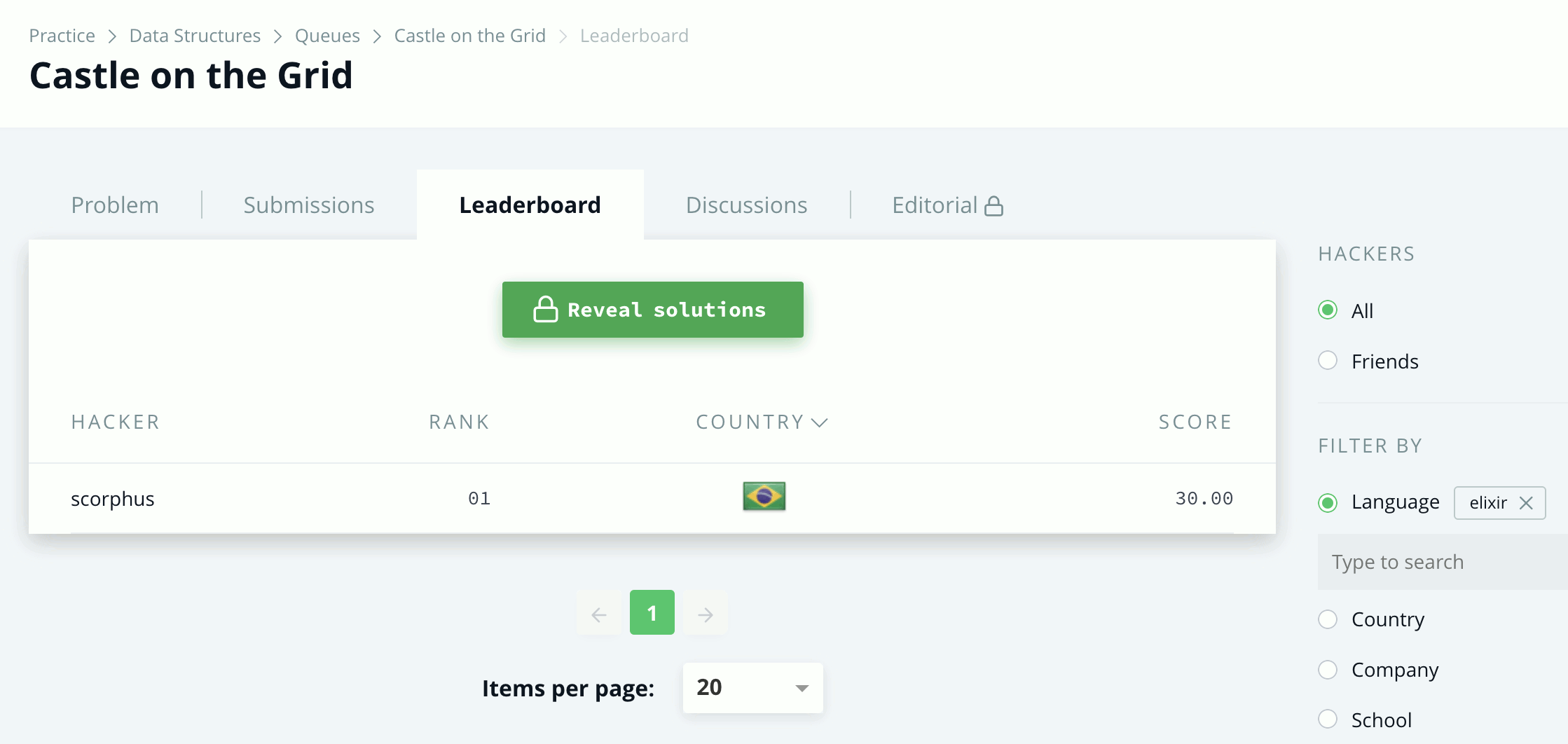
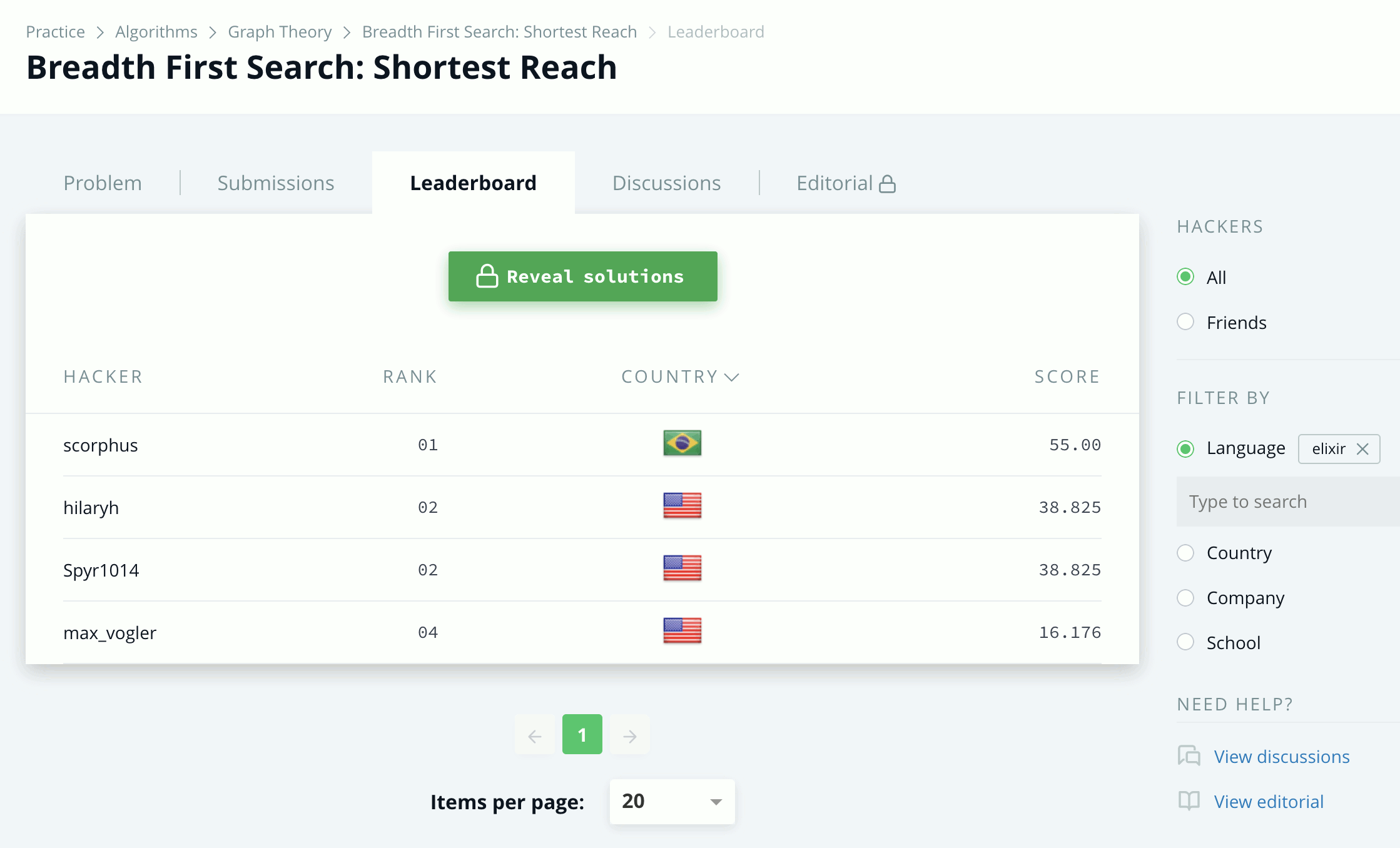
In the first problem, you’re given a grid with some obstacles, and you need to find the cost of the shortest path from one cell to another, while in the second one you are given several nodes and edges, and you must find the cost of the shortest path from a start node to every other node in the graph. Being a more generic BFS implementation, the solution to Shortest Reach is the one I’ll discuss below.
The input is in the following form:
<number_of_graphs>
<number_of_nodes> <number_of_edges>
<edge_from_node> <edge_to_node>
<start_node>
For example:
2 # There are two graphs (or queries as the problem describes)
4 2 # 4 nodes and 2 edges for 1st graph
1 2 # An edge from node 1 to node 2
1 3 # An edge from node 1 to node 3
1 # Starting from node 1
3 1 # 3 nodes and 1 edge for 2nd graph
2 3 # An edge from node 2 to node 3
2 # Starting from node 2
Reading from input
Spoiler alert: pause now if you’d like to solve any of the problems.
The solution consists of a module, ShortestReach, with a bunch of small functions with well-defined responsibilities. Frequently, that’s what you aim for when working with a functional language. main’s job is to read the first line, remove any blank spaces or newlines, convert it to an integer, and pipe the result into shortest_reach:
1defmodule ShortestReach do
2 def main do
3 IO.gets("")
4 |> String.trim()
5 |> String.to_integer()
6 |> shortest_reach()
7 end
It’s up to shortest_reach to do a sequence of things for every graph – or query, hence q – until there are no more graphs left to process:
9 defp shortest_reach(0) do
10 end
11
12 defp shortest_reach(q) do
13 [n, m] =
14 IO.gets("")
15 |> String.trim()
16 |> String.split(" ")
17 |> Enum.map(&String.to_integer/1)
18
19 [nil | edges] = read_edges(nil, m)
20
21 # the start node should be read before adding any
22 # edge to avoid adding edges from any node back
23 # to the start node, as that would be wasteful
24 s =
25 IO.gets("")
26 |> String.trim()
27 |> String.to_integer()
28
29 init_graph(n)
30 |> add_edges(edges, s)
31 |> bfs(s)
32 |> expand_paths(n, s)
33 |> Enum.reverse()
34 |> Enum.join(" ")
35 |> IO.puts()
36
37 shortest_reach(q - 1)
38 end
The next function reads m edges from the input:
40 defp read_edges(edges, 0), do: [edges]
41
42 defp read_edges(edges, m) do
43 [
44 edges
45 | IO.gets("")
46 |> String.trim()
47 |> String.split(" ")
48 |> Enum.map(&String.to_integer/1)
49 |> read_edges(m - 1)
50 ]
51 end
Did you notice that a new edge is prepended to the list instead of appended? It’s an important detail to observe. Elixir variables are immutable, and because of that, whenever a list a receives another b to appended, like in a ++ b, a first needs to be copied into a new list before appending b. That becomes a problem as a increases in length. It’s best if you always consider prepending instead. If edges were appended, the solution wouldn’t run under time limits for some cases. Have a look at the docs for more.
Moving on to init_graph, it’s responsible for initializing the graph with all the n nodes, each of them with an empty set of immediate neighbor nodes. A MapSet is used here to ensure that each neighbor node is unique in cases of duplicate edges. This is, in fact, key for the solution to run under the limits set by HackerRank.
53 defp init_graph(0), do: %{0 => MapSet.new()}
54 defp init_graph(n), do: init_graph(n - 1) |> Map.put(n, MapSet.new())
Pattern matching FTW!

With the graph initialized, the edges can now be processed. Adding an edge back to the start node would be wasteful. So, whenever you encounter an edge involving the start node, you should add only the other node of the edge as an immediate neighbor of the start node. That’s what the second and third functions are doing.
56 defp add_edges(graph, [], _), do: graph
57
58 # add only v as immediate neighbor of s
59 defp add_edges(graph, [[s, v] | edges_tail], s) do
60 Map.put(graph, s, MapSet.put(graph[s], v))
61 |> add_edges(edges_tail, s)
62 end
63
64 # add only u as immediate neighbor of s
65 defp add_edges(graph, [[u, s] | edges_tail], s) do
66 Map.put(graph, s, MapSet.put(graph[s], u))
67 |> add_edges(edges_tail, s)
68 end
69
70 # add u and v as immediate neighbors of each other
71 defp add_edges(graph, [[u, v] | edges_tail], s) do
72 Map.put(graph, u, MapSet.put(graph[u], v))
73 |> Map.put(v, MapSet.put(graph[v], u))
74 |> add_edges(edges_tail, s)
75 end
Take a moment to marvel at how pattern matching shines here! At this point, you have already noticed that the order in which the functions are declared matters.
Breadth-first search
Great! All of this to load the graph into memory! Now the breadth-first search can finally take place. It receives the initialized graph and the start node – bfs(graph, s) – and initiates the “real” BFS, as you’ll see later.
The goal of bfs is to return a Map, paths, in which the key is a node, and the value is the number of edges from s to that node. Take the following graph as an example:
The output of bfs(graph, 1) for that graph would be:
%{
2 => 1,
3 => 1,
4 => 1,
6 => 2,
7 => 2,
8 => 1,
9 => 3,
10 => 3,
11 => 2,
12 => 2
}
To do that, bfs needs to visit all nodes that are on the same neighboring layer of s before advancing to the next layer. For every new node, it registers its distance from s as the number of layers advanced until then. Starting from the “generic” bfs/2 function, it bootstraps the BFS with five arguments, as per the comments:
77defp bfs(graph, s) do
78 # bootstrap the BFS with:
79 # - an empty map
80 # - the initialized graph
81 # - the list of neighbors of `s`
82 # - an empty list of nodes to visit next
83 # - the initial layer
84 bfs(%{}, graph, MapSet.to_list(graph[s]), [], 1)
85end
Now, for every layer, there is a list of nodes to be visited. bfs/5 visits them one by one, using the [head | tail] pattern matching. For every unvisited node – one not yet in the paths map – its immediate neighbors are added to a list of nodes, neighbors, to be visited in the next layer. Once tail becomes an empty list, it means that there are no more unvisited nodes in that layer, and the BFS can proceed to the next one. That’s when the layer is incremented, and the accumulated neighbors are, in turn, visited. This process repeats until both lists are empty, and paths is returned. See how pattern matching makes Elixir declarative:
87defp bfs(paths, _, [], [], _), do: paths
88
89defp bfs(paths, graph, [], neighbors, layer) do
90 bfs(paths, graph, neighbors, [], layer + 1)
91end
92
93defp bfs(paths, graph, [u | tail], neighbors, layer) do
94 cond do
95 Map.has_key?(paths, u) ->
96 bfs(paths, graph, tail, neighbors, layer)
97
98 true ->
99 Map.put_new(paths, u, layer)
100 |> bfs(graph, tail, MapSet.to_list(graph[u]) ++ neighbors, layer)
101 end
102end
With that, bfs returns paths. It has the number of edges from s to each of the reachable nodes in the graph. That would be the solution if the problem statement didn’t add a small detail: the cost of an edge is 6 units, and, for every unreachable node, the cost is -1. The last function, expand_paths, takes care of that:
116defp expand_paths(_, 0, _), do: []
117
118defp expand_paths(paths, s, s), do: expand_paths(paths, s - 1, s)
119
120defp expand_paths(paths, n, s) do
121 cond do
122 Map.has_key?(paths, n) ->
123 [paths[n] * 6] ++ expand_paths(paths, n - 1, s)
124
125 true ->
126 [-1] ++ expand_paths(paths, n - 1, s)
127 end
128end
Wouldn’t it be nice to have a guard that could check whether n is a key of paths? The good news is that the next version of Elixir, v1.10, will allow that! The first release candidate was drafted a few days ago. It requires Erlang/OTP 21+ and brings with it two new guards, is_map_key/2 and map_get/2. Once it’s released, bfs/5 and expand_paths/3 can be refactored into much more readable, declarative versions:
87defp bfs(paths, _, [], [], _), do: paths
88
89defp bfs(paths, graph, [], neighbors, layer) do
90 bfs(paths, graph, neighbors, [], layer + 1)
91end
92
93defp bfs(paths, graph, [u | tail], neighbors, layer) when is_map_key(paths, u) do
94 bfs(paths, graph, tail, neighbors, layer)
95end
96
97defp bfs(paths, graph, [u | tail], neighbors, layer) do
98 Map.put_new(paths, u, layer)
99 |> bfs(graph, tail, MapSet.to_list(graph[u]) ++ neighbors, layer)
100end
101
102defp expand_paths(_, 0, _), do: []
103
104defp expand_paths(paths, s, s), do: expand_paths(paths, s - 1, s)
105
106defp expand_paths(paths, n, s) when is_map_key(paths, n) do
107 [paths[n] * 6] ++ expand_paths(paths, n - 1, s)
108end
109
110defp expand_paths(paths, n, s) do
111 [-1] ++ expand_paths(paths, n - 1, s)
112end
I hope you noticed that expand_paths prepends costs. That’s why they get reversed on line 33. With that, the Shortest Reach solution for the graph presented above is:
6 6 6 -1 12 12 6 18 18 12 12
Wrap up

As you could certainly attest, my holidays were packed with fun! Despite my devotion to learning this fantastic language, I had some cool outdoor activities and even a short trip to Salzburg with my lovely wife, which we both enjoyed a lot.
I hope you enjoyed the contents of this post. Here you can find the complete solution and below a REPL for you to experiment with. I’d love to read your thoughts on the comments section at the bottom. In case you spotted anything I could have done differently or better, I’d be more than grateful if you could share your ideas.
1defmodule ShortestReach do
2 def main do
3 IO.gets("")
4 |> String.trim()
5 |> String.to_integer()
6 |> shortest_reach()
7 end
8
9 defp shortest_reach(0) do
10 end
11
12 defp shortest_reach(q) do
13 [n, m] =
14 IO.gets("")
15 |> String.trim()
16 |> String.split(" ")
17 |> Enum.map(&String.to_integer/1)
18
19 [nil | edges] = read_edges(nil, m)
20
21 # the start node should be read before adding any
22 # edge to avoid adding edges from any node back
23 # to the start node, as that would be wasteful
24 s =
25 IO.gets("")
26 |> String.trim()
27 |> String.to_integer()
28
29 init_graph(n)
30 |> add_edges(edges, s)
31 |> bfs(s)
32 |> expand_paths(n, s)
33 |> Enum.reverse()
34 |> Enum.join(" ")
35 |> IO.puts()
36
37 shortest_reach(q - 1)
38 end
39
40 defp read_edges(edges, 0), do: [edges]
41
42 defp read_edges(edges, m) do
43 [
44 edges
45 | IO.gets("")
46 |> String.trim()
47 |> String.split(" ")
48 |> Enum.map(&String.to_integer/1)
49 |> read_edges(m - 1)
50 ]
51 end
52
53 defp init_graph(0), do: %{0 => MapSet.new()}
54 defp init_graph(n), do: init_graph(n - 1) |> Map.put(n, MapSet.new())
55
56 defp add_edges(graph, [], _), do: graph
57
58 # add only v as immediate neighbor of s
59 defp add_edges(graph, [[s, v] | edges_tail], s) do
60 Map.put(graph, s, MapSet.put(graph[s], v))
61 |> add_edges(edges_tail, s)
62 end
63
64 # add only u as immediate neighbor of s
65 defp add_edges(graph, [[u, s] | edges_tail], s) do
66 Map.put(graph, s, MapSet.put(graph[s], u))
67 |> add_edges(edges_tail, s)
68 end
69
70 # add u and v as immediate neighbors of each other
71 defp add_edges(graph, [[u, v] | edges_tail], s) do
72 Map.put(graph, u, MapSet.put(graph[u], v))
73 |> Map.put(v, MapSet.put(graph[v], u))
74 |> add_edges(edges_tail, s)
75 end
76
77 defp bfs(graph, s) do
78 # bootstrap the BFS with:
79 # - an empty map
80 # - the initialized graph
81 # - the list of neighbors of `s`
82 # - an empty list of nodes to visit next
83 # - the initial layer
84 bfs(%{}, graph, MapSet.to_list(graph[s]), [], 1)
85 end
86
87 defp bfs(paths, _, [], [], _), do: paths
88
89 defp bfs(paths, graph, [], neighbors, layer) do
90 bfs(paths, graph, neighbors, [], layer + 1)
91 end
92
93 defp bfs(paths, graph, [u | tail], neighbors, layer) do
94 cond do
95 Map.has_key?(paths, u) ->
96 bfs(paths, graph, tail, neighbors, layer)
97
98 true ->
99 Map.put_new(paths, u, layer)
100 |> bfs(graph, tail, MapSet.to_list(graph[u]) ++ neighbors, layer)
101 end
102 end
103
104 defp expand_paths(_, 0, _), do: []
105
106 defp expand_paths(paths, s, s), do: expand_paths(paths, s - 1, s)
107
108 defp expand_paths(paths, n, s) do
109 cond do
110 Map.has_key?(paths, n) ->
111 [paths[n] * 6] ++ expand_paths(paths, n - 1, s)
112
113 true ->
114 [-1] ++ expand_paths(paths, n - 1, s)
115 end
116 end
117end
118
119ShortestReach.main()
You can experiment with the solution using the following REPL:
About the author
Pablo Aguiar is a software engineer and coffee geek from Brazil. He's curious about computers, maths and science. He enjoys a good coffee and loves literature. Read more...